W czasach licealnych trafiłem na obóz szkoleniowy dla kandydatów na międzynarodową olimpiadę matematyczną. A tam, oprócz brydża, łażenia po górach i wykładów miał miejsce swoisty maraton zadaniowy, codziennie dostawaliśmy po kilka zadań a potem dyskutowaliśmy ich rozwiązania.
Był to jeden z kulminacyjnych punktów obszernego cyklu kółek, seminariów i konkursów organizowanych dla uzdolnionych matematycznie licealistów. Grupa matematyków uniwersyteckich wkładała w to naprawdę dużo serca i pracy - i tworzyli coś bardzo ciekawego.
Zadania były trudne ale każde choć kilka osób zrobiło. Zdziwiliśmy się więc, gdy któregoś dnia w miarę łagodnie wyglądające zadanko z geometrii poprawnie rozwiązał tylko jeden z nas. Okazało się, że ... miał cyrkiel i zrobił porządny rysunek.
W tym artykule parę słów o cyrklu, którego obecnie używam do rozwiązywania zadanek geometrycznych, czyli o paru Linuxowych programach pozwalających wygodnie malować przecinające się pod różnymi kątami proste, okręgi wpisane i opisane, dwusieczne, spodki wysokości i inne elementy eksploatowane w geometrii planarnej.
Kig
Kig to łatwy i intuicyjny program do malowania myszą. Rozwodziłem się ostatnio o robieniu screencastów pod Linuxem, dlatego zamiast opisu ruchome obrazki.
Parę miesięcy temu w Delcie było takie zadanie:
Punkt D leży na boku BC trójkąta ABC, w którym |AB| = |AC|. Punkt F leży na okręgu opisanym na trójkącie ACD, wewnątrz trójkąta ABC. Okrąg przechodzący przez punkty B, D, F przecina bok AB w punkcie E. Dowieść, że
|CD| |EF| + |DF| |AE| = |BD| |AF|
Zrobię sobie do niego rysunek.
KIG screencast from Mekk on Vimeo.
(lepsza jakość: plik AVI 8MB).
Eukleides
Zupełnie inne podejście reprezentuje Eukleides. Tutaj zamiast machać myszą, piszemy coś pośredniego między listą wzorów, a prostym programem. Czasem tak jest wygodniej (a do tego można wykorzystać to narzędzie przy wsadowej generacji dokumentów skryptami).
Jakiś czas temu malowałem sobie przy jego pomocy takie zadanie (także z Delty):
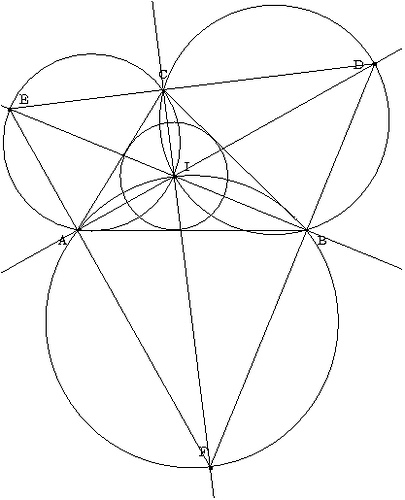
Punkt I jest środkiem okręgu wpisanego w trójkąt ABC. Prosta AI przecina okrąg opisany na trójkącie BIC w punktach I i D; prosta BI przecina okrąg opisany na trójkącie CIA w punktach I i E; prosta CI przecina okrąg opisany na trójkącie AIB w punktach I i F. Wyznaczyć największą możliwą wartość iloczynu |AI| / |AD| * |BI| / |BE| * |CI| / |CF|.
Oto jak wyglądał zapis w slangu Eukleidesa:
frame(-2,-7,8.5,6)
A B C triangle
draw(A,B,C)
draw("A",A, 213:)
draw("B", B, -33:)
draw("C", C, 90:)
inc = incircle(A,B,C)
draw(inc)
I = center(inc)
draw(I)
draw("I", I, 33:)
a_i = line(A,I)
b_i = line(B,I)
c_i = line(C,I)
draw(a_i)
draw(b_i)
draw(c_i)
o_bic = circle(B,I,C)
o_aic = circle(A,I,C)
o_aib = circle(A,I,B)
draw(o_bic)
draw(o_aic)
draw(o_aib)
NU D intersection(a_i,o_bic)
NU E intersection(b_i,o_aic)
NU F intersection(c_i,o_aib)
draw("D",D,183:)
draw(D)
draw("E",E,33:)
draw(E)
draw("F",F,113:)
draw(F)
draw(segment(D,E))
draw(segment(E,F))
draw(segment(D,F))
Powyższe zapisane w pliku tekstowym - powiedzmy rysunek.euk.
A następnie, do wyboru:
$ euk2eps rysunek.euk
(powstanie plik rysunek.eps) albo, jeśli piszemy dokument
w LaTeXu:
$ eukleides rysunek.euk > rysunek.tex
(powstanie fragment, który można wstawić w tekst pisany w LaTeXu).
Efekt:
Podsumowanie
Podobnych programów jest jeszcze parę, te dwa mi spodobały się najbardziej. Rzutu okiem jest na pewno wart także DrGeo.
Przydadzą się komuś hobbistycznie rozwiązującemu zadanka, uczniowi czy studentowi robiącemu je ... mniej hobbistycznie, wreszcie - nauczycielowi czy korepetytorowi.
Aha: wszystkie powyższe programy są dostępne w paczkach (przynajmniej na Ubuntu i Debianie):
$ sudo apt-get install kig eukleides drgeo