Bardzo mądry kalkulator

Było już o cyrklu (czyli o narzędziu do rysunków geometrycznych), dzisiaj o kalkulatorze. Bardzo mądrym kalkulatorze, pomagającym nie tylko w prostych obliczeniach ale i nietrywialnych przekształceniach algebraicznych czy analitycznych. Od rachunków na ułamkach po przestrzenie macierzy. Od rozwiązań prostych równań po krzywe eliptyczne.

Sage

Chodzi mi o Sage. Alternatywę open source dla programów takich, jak Mathematica, Maple czy Matlab. Środowisko, w którym wiedza matematyczna została obudowana dookoła interpretera Pythona.

Nie pokuszę się tu o pełny opis funkcjonalności, w sporej mierze wykraczającej zresztą poza mój aparat matematyczny. Patrz dokumentacja. Zamiast tego dam parę przykładów na zachętę.

Kilka przykładów użycia Sage

Rachunki

Zacznijmy od rachunków na ułamkach. Nic wielkiego ale…

sage: 1/9 + 5/24
23/72
sage: 1/9 + 4/(81*7) + (2/21) + (1/2)^4
2503/9072
sage: 1/10000000000000000000000000 * 5^25
1/33554432

Oczywiście można przeliczyć na rozwinięcie dziesiętne (n to funkcja wyliczająca numeryczne przybliżenie dowolnego wyrażenia):

sage: n(1/9 + 5/24)
0.319444444444444
sage: n(1/9 + 4/(81*7) + (2/21) + (1/2)**4)
0.275903880070547
sage: n( (1+1/100)^100 )
2.70481382942153

Mamy różne popularne funkcje i stałe:

sage: sin(pi/3)
sqrt(3)/2
sage: tan(pi/4)
1
sage: sin(pi/3) ** 2 + cos(pi/3) ** 2
1
sage: factorial(32)
263130836933693530167218012160000000

Liczby pierwsze, rozkłady, funkcja π(n), dzielniki:

sage: is_prime(997)
True
sage: print list(primes(30))
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
sage: prime_powers(30)
[1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29]
sage: prime_pi(100)
25
sage: prime_factors(992)
[2, 31]
sage: factor(992)
2^5 * 31
sage: gcd(100,160)
20

Arytmetyka modularna:

sage: M17 = Integers(17)
sage: M17(19)
2
sage: M17(2) ** 16
1
sage: M18 = Integers(18)
sage: M18(2) ** 10000000000000000000000000
16
sage: euler_phi(1001)
720
sage: euler_phi(997)
996

Kombinatoryka:

sage: p = Permutations(3)
sage: p.list()
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

sage: number_of_combinations([1,2,3,4,5,6], 3)
20
sage: number_of_combinations([1,2,3,4,5,5], 3)
14

sage: Subwords("abc").list()
[[], ['a'], ['b'], ['c'], ['a', 'b'], ['a', 'c'], ['b', 'c'], ['a', 'b', 'c']]

Obliczenia zmiennoprzecinkowe z zadaną dokładnością:

sage: RZ = RealField(32)
sage: RZ
Real Field with 32 bits of precision
sage: RZ(pi)
3.14159265
sage: RZ(1)/3
0.333333333

sage: RealField(800)(2)^(1/2)
1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038753432764157273501384623091229702492483605585073721264412149709993583141322266592750559275579995050115278206057147010955997160597027453459686201472851742

I dużo, dużo więcej...

Przekształcenia symboliczne

Mnożenie, dzielenie, rozkładanie, składanie wielomianów jednej i wielu zmiennych:

sage: factor(x^2 + 2*x + 1)
(x + 1)^2
sage: expand( (x+1)^7 )
x^7 + 7*x^6 + 21*x^5 + 35*x^4 + 35*x^3 + 21*x^2 + 7*x + 1

sage: f(x) = (12*x^2 + 5*x - 2)*(7 * x^2 + 9)
sage: f.factor()
84*(x - 1/4)*(x + 2/3)*(x^2 + 9/7)
sage: f.expand()
x |--> 84*x^4 + 35*x^3 + 101*x^2 + 45*x - 9

sage: s(x,y) = (x+1)*(y+1) - (x-1)*(y-1)
sage: s
(x, y) |--> (x + 1)*(y + 1) - (x - 1)*(y - 1)
sage: s.expand()
(x, y) |--> 2*y + 2*x

Funkcje wymierne:

sage: f(x,y,z) = (x + y + z)/(x^2 + y^2 + z^2)    
sage: f
(x, y, z) |--> (z + y + x)/(z^2 + y^2 + x^2)
sage: g(x,y,z) = (x * y * z)/( (1+x)*(1+y)*(1+z) )
sage: g
(x, y, z) |--> x*y*z/((x + 1)*(y + 1)*(z + 1))
sage: f + g
(x, y, z) |--> (z + y + x)/(z^2 + y^2 + x^2) + x*y*z/((x + 1)*(y + 1)*(z + 1))
sage: (f+g).expand()  
(x, y, z) |--> z/(z^2 + y^2 + x^2) + y/(z^2 + y^2 + x^2) + x/(z^2 + y^2 + x^2) + x*y*z/(x*y*z + y*z + x*z + z + x*y + y + x + 1)
sage: (f+g)(x,x,x)
x^3/(x + 1)^3 + 1/x
sage: f(1/8)
(z + y + 1/8)/(z^2 + y^2 + 1/64)
sage: f(1/8,1/4,1/2)
8/3

Przekształcenia wykorzystujące funkcje trygonometryczne, logarytmiczne i inne:

sage: (1 - sin(x)^2).simplify_trig()
cos(x)^2

sage: exp( (1-ln(1+3*x)) )
e/(3*x + 1)

Różniczkowanie i całkowanie symboliczne:

sage: h(x) = ln(x+1) - ln(x-1)
sage: h
x |--> log(x + 1) - log(x - 1)
sage: h.differentiate()
x |--> 1/(x + 1) - 1/(x - 1)
sage: h.differentiate(4)
x |--> 6/(x - 1)^4 - 6/(x + 1)^4

sage: h.integrate()
x |--> (x + 1)*log(x + 1) - (x - 1)*log(x - 1) - 2

Rozwiązywanie równań:

sage: solve(5*x*x + 3*x - 1 == 0)
[x == (-sqrt(29) - 3)/10, x == (sqrt(29) - 3)/10]

sage: f(x,y,z) = (x+y+z)*(x*y + x*z + y*z)
sage: solve(f(x,y,z) == 0, z)
[z == -x*y/(y + x), z == -y - x]

sage: solve( cos(x) == 1/2 )
[x == pi/3]

Wyliczanie granic:

sage: limit(sin(x^2)/x^2, x = 0)
1
sage: limit( (7^x + 3*x^3)^(1/x), x = oo)
7

Analiza

Numeryczne rozwiązania równań:

sage: find_root( (sin(x)/x)^4 - cos(x), 0.001, pi/2-0.001 )
1.1944543491329256

Numeryczne całkowanie:

sage: f(x) = exp(sin(x))
sage: f.nintegral(x,0,1)
(1.6318696084180511, 1.8117392124517591e-14, 21, 0)

(kolejno: wynik, szacowany błąd i dodatkowe informacje o przebiegu algorytmu)

Obliczenia asymptotyczne:

sage: f(x) = 1 + 2 * x - 3 * x^2
sage: g = f.power_series(QQ)    
sage: g
1 + 2*x - 3*x^2 + O(x^3)
sage: g^3                       
1 + 6*x + 3*x^2 + O(x^3)

Rozwinięcia w szereg Taylora:

sage: sin(x).taylor(x, 0, 6)
x - x^3/6 + x^5/120

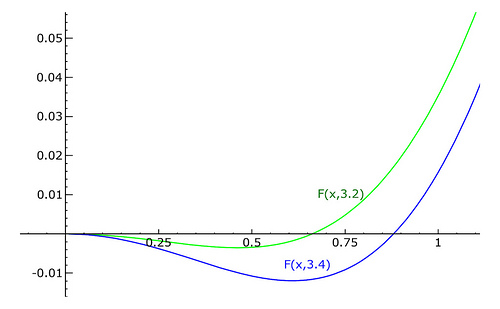
Wykresy:

sage: F(x,y) = (sin(x)/x)^y - cos(x)
sage: P2 = plot(F(x,3.2), (0.01, pi/2-0.01), color='green')
sage: P4 = plot(F(x,3.4), (0.01, pi/2-0.01), color='blue')
sage: Q2 = text("F(x,3.2)", (0.74,0.01), rgbcolor='green')
sage: Q4 = text("F(x,3.4)", (0.65,-0.008), rgbcolor='blue')
sage: (P2+P4+Q2+Q4).show(xmin=-0.02,xmax=1,
                         ymin=-0.01,ymax=0.05,dpi=300)

I tak dalej...

Tryby pracy

Sage można wykorzystywać na trzy sposoby: przy użyciu konsoli, za pośrednictwem graficznego notatnika oraz jako język programowania.

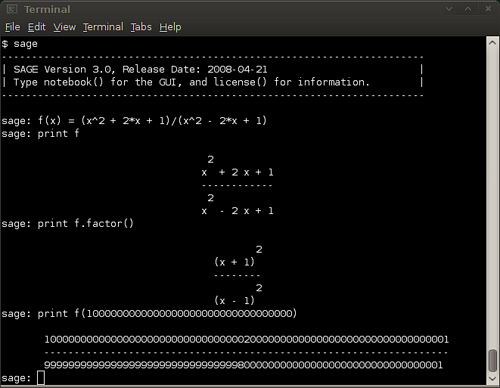
Konsola

Konsola Sage - uruchamiana poleceniem sage - to interaktywny intepreter poleceń (pochodzą z niego wszystkie powyższe przykłady). Bardzo wygodny w użyciu dzięki:

• dopełnaniu tabulatorem (najprostszy sposób by zobaczyć, co można zrobić z funkcją f, to napisać f. i nacisnąć Tab),

• kontekstowej pomocy (jeśli nie wiem, jak działa funkcja plot, to piszę plot? i dostaję szczegółowy opis),

• historii poleceń i edycji linii komend.

Konsola Sage jest oparta o ipython, używa się jej tak samo.

Notatnik

Polecenie

sage: notebook()

uruchamia graficzny notatnik. Dokładniej: uruchamia wbudowany serwer HTTP obsługujący webową aplikację Sage, a następnie otwiera przeglądarkę na jej głównej stronie.

Pierwsze uruchomienie notebook() spowoduje zadanie kilku pytań dotyczących konfiguracji tego serwera. O ile nie chcemy udostępniać notatnika w sieci, wystarczy naciskać Enter.

Notatnik Sage posługuje się metaforą arkuszy. Każdy arkusz to osobny zbiór zmiennych, funkcji i wyrażeń, które mogą być ze sobą powiązane. Arkusze są zapisywane na dysku (domyślnie w katalogu ~/.sage/sage_notebook/worksheets) i można do nich wrócić po restarcie sage.

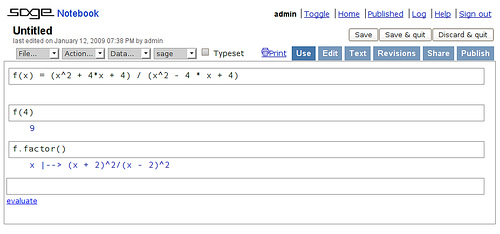
Osobiście preferuję konsolę ale notatnik też ma swoje zalety: dzięki opcjom zapisu/odczytu arkuszy pozwala wielokrotnie wracać do tej samej sesji, wszystkie elementy są naraz widoczne, przy odrobinie wysiłku konfiguracyjnego można je współdzielić z innymi osobami. A szczególnie przydatna jest opcja Action/Evaluate All (przeliczenie wszystkich wyrażeń): np. jeśli zdefiniowałem jakąś funkcję i stworzyłem różne wyrażenia na jej podstawie, mogę skorygować definicję i jednym ruchem przeliczyć wszystko od nowa.

Język programowania

Sage jest też językiem programowania. Językiem będącym rozszerzeniem Pythona i programowalnym w ten sam sposób. Można zatem pisać skrypty .sage i je uruchamiać. W skryptach tych można wykorzystywać zwykłe Pythonowe zmienne, pętle, funkcje, klasy, generatory, można importować moduły biblioteki standardowej - co komu przyjdzie do głowy.

Prymitywny przykład - szukamy sumy początkowych liczb pierwszych, której ostatnie trzy cyfry są zerami:

def primes_sum(zero):
    total = zero
    for p in Primes():
        total += p
        yield p, total

MAX = 10^3
IV = Integers(MAX)
ZERO = IV(0)
for p, s in primes_sum(ZERO):
    if s == 0:
       print "2 + 3 + ... + %d = 0 (mod %d)" % (p, MAX)
       break

generator primes_sum nie jest tu tak naprawdę potrzebny, zamieściłem go jako ilustrację definiowania funkcji.

Powyżej z Sage użyłem generatora liczb pierwszych (Primes()) oraz arytmetyki modularnej (pierścień Integers(1000)). Równie dobrze mogłem - na przykład - definiować coraz to inne funkcje i szukać ich pierwiastków.

Taki skrypt uruchamiamy pisząc po prostu (o ile został zapisany jako skrypt.sage):

$ sage skrypt.sage

Efekt:

2 + 3 + ... + 35677 = 0 (mod 1000)

Uwaga: skryptu nie należy zapisywać z rozszerzeniem .py. Pierwszym etapem działania sage jest stworzenie pliku o tym rozszerzeniu (tu: skrypt.py), który następnie jest uruchamiany.

Podsumowując: na programowanie w Sage należy patrzeć jak na programowanie w Pythonie (zresztą, Sage uruchomi poprawnie większość skryptów Pythonowych) - tyle, że mamy do dyspozycji pokaźną funkcję klas, funkcji i obiektów reprezentujących byty matematyczne.

Sage wewnętrznie

Część elementów Sage została zaimplementowana na potrzeby tego projektu ale przede wszystkim jest to projekt integracyjny, zbierający w jeden spójny pakiet cały szereg bibliotek i programów pomocniczych - tak pythonowych (choćby sympy czy numpy) jak innych (GAP, Maxima, GP/Pari i wiele innych).

Sage potrafi opakować nawet Mathematicę i Matlaba - oczywiście o ile się je posiada.

Całość jest silnie zoptymalizowana (Sage jest jednym z projektów napędzających rozwój Cythona) ale główną wartością projektu jest zebranie chmary komponentów, doprowadzenie ich do współdziałania i przedstawienie w naturalnej w użyciu formie.

Sage a Python

Czym Sage różni się od Pythona?

Oczywistą różnicą jest obszerny zbiór predefiniowanych i preimportowanych klas, funkcji i obiektów reprezentujących różne byty matematyczne.

Dochodzą do tego drobne zmiany parsera (tak naprawdę - preprocessing). Służy on głównie do przepakowania stałych numerycznych jako obiektów (np. 97 staje się Integer(97), dzięki czemu 97/13 będzie ułamkiem, a nie liczbą 7). Podobnie, zapisy definiujące funkcje są konwertowane na wywołania funkcji symbolic_expression. Zmienia się semantyka niektórych operatorów (w szczególności ^ jest traktowane jako potęgowanie).

Pouczające jest porównanie pliku .sage z wygenerowanym w czasie uruchamiania plikiem .py. Dla cytowanego wyżej skrypt.sage powstał następujący skrypt.py:

# This file was *autogenerated* from the file skrypt.sage.
from sage.all_cmdline import *   # import sage library

def primes_sum(zero):
    total = zero
    for p in Primes():
        total += p
        yield p, total

MAX = Integer(10)**Integer(3)
IV = Integers(MAX)
ZERO = IV(Integer(0))
for p, s in primes_sum(ZERO):
    if s == Integer(0):
       print "2 + 3 + ... + %d = 0 (mod %d)" % (p, MAX)
       break

Tu zmiany są minimalne. Definiujący funkcję skrypt:

f(x) = x * sin(x)
print f(ln(x))

po przetłumaczeniu na goły Python ma formę:

# This file was *autogenerated* from the file skrypt2.sage.
from sage.all_cmdline import *   # import sage library

_=var("x");f=symbolic_expression(x * sin(x)).function(x)
print f(ln(x))

Wreszcie, ponieważ Sage wykorzystuje własny (stanowiący element dystrybucji) interpreter Pythona, mogą występować drobne różnice w zawartości biblioteki standardowej.

Instalacja pod Linuksem

Jeszcze dopisek o instalacji. Ściągamy binarny pakiet ze strony projektu - uważnie wybierając odpowiednią wersję (to jest w tej chwili prawie 400 megabajtów).

Można kompilować wersję źródłową ale trwa to bardzo, bardzo długo. Pozytywny element: dystrybucja Sage zawiera niemal wszystkie potrzebne biblioteki i komponenty, zewnętrzne zależności ograniczają się do kompilatora i biblioteki standardowej.

Następnie rozpakowujemy go i tworzymy link symboliczny gdzieś w ścieżce, np:

$ cd ~
$ tar xzvf ~/Download/sage-3.2.2-ubuntu32bit-intel-i686-Linux.tar.gz
...
$ ln -s ~/sage-3.2.2-ubuntu32bit-intel-i686-Linux/sage    ~/bin/

i uruchamiamy:

$ sage

Przy pierwszym uruchomieniu Sage będzie generować rozmaite pliki w drzewie instalacji (min. skompilowane wersje modułów pythonowych), co może potrwać kilka minut.

Sage sprawia trochę problemów przy próbach instalowania plików jako własności root-a, od czasu do czasu zmienia pliki w swoim drzewie instalacji (dotyczy to tworzenia .pyc i .pyo ale też dogrywania rozszerzeń i paru innych zmian). Nie ćwiczyłem tego, chcącym się pokusić o ten rodzaj instalacji radziłbym zainstalować z uprawnieniami użytkownika, uruchomić sage po raz pierwszy i dopiero potem zmieniać właściciela plików na root-a.

Inne możliwości instalacji i używania

Sage jest dostępne także dla Solarisa i Mac OS X. Wersji dla Windows nie ma ale można pobrać gotowy obraz dla VirtualBoksa zawierający okrojoną dystrybucję Linuksa z preinstalowanym i skonfigurowanym Sage. Wszystkie te dystrybucje można pobrać z tej strony

Z kolei na stronie sagenb.org działa ogólnodostępny notebook, z którego można korzystać online.